Решение логических задач методом графа

 

В течение всех лет обучения в школе мы много решаем разнообразных задач, в том числе и логических: задачи занимательного характера, головоломки, анаграммы, ребусы и т.п. Чтобы успешно решать задачи такого вида, надо уметь выделять их общие признаки, подмечать закономерности, выдвигать гипотезы, проверять их, строить цепочки рассуждений, делать выводы. Логические задачи от обычных отличаются тем, что не требуют вычислений, а решаются с помощью рассуждений. Можно сказать, что логическая задача – это особая информация, которую не только нужно обработать в соответствии с заданным условием, но и хочется это сделать. Логика помогает усваивать знания осознанно, с пониманием, т.е. не формально; создаёт возможность лучшего взаимопонимания.

Логика – это искусство рассуждать, умение делать правильные выводы. Это не всегда легко, потому что очень часто необходимая информация "замаскирована", представлена неявно, и надо уметь её извлечь. Как известно, видение рождает мышление. Возникает проблема: как установить логические связи между разрозненными фактами и как оформить в виде единой целой. Видеть ход доказательства и решения задач позволяет метод граф - схем, который делает доказательство более наглядным и позволяет кратко и точно изложить доказательства теорем и решения задач.

Задача 1. Красный, синий, желтый и зеленый карандаши лежат в четырех коробках по одному. Цвет карандаша отличается от цвета коробки. Известно, что зеленый карандаш лежит в синей коробке, а красный не лежит в желтой. В какой коробке лежит каждый карандаш?

Решение. Обозначим точками карандаши и коробки. Сплошная линия будет обозначать, что карандаш лежит в соответствующей коробке, а пунктирная, что не лежит. Тогда с учетом задачи имеем G1 (рис. 1).

 

 

Рис.1

 

Далее достраиваем граф по следующему правилу: поскольку в короб может лежать ровно один карандаш, то из каждой точки должны выходить одна сплошная линия и три пунктирные. Получается граф G2 , дающий решение задачи.

Задача 2. Беседуют трое друзей: Белокуров, Чернов и Рыжов. Брюнет сказал Белокурову: "Любопытно, что один из нас белокурый, другой брюнет, третий рыжий, но ни у кого цвет волос не соответствует фамилии". Какой цвет волос имеет каждый из друзей?

Решение. Построим граф отношения, заданного в условии задачи. Для этого, прежде всего, выделим множество фамилий М и множество цветов волос К, элементы которых будем обозначать точками. Точки множества М назовем буквами Б, Ч, Р (Белокуров, Чернов и Рыжов); точки второго множества – б, бр, р (белокурый, брюнет, рыжий). Если точке из одного множества соответствует точка из другого, мы их соединим сплошной линией, а если не соответствует – штриховой. Условие задачи указывает лишь на несоответствия, поэтому вначале должен возникнуть граф, изображенный на рисунке 2.

 

 

 

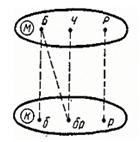
Рис.2

 

Из условия задачи следует, что для каждой точки из множества М существует одна и только одна точка из множеств К, которая соответствует первой и, наоборот, каждой точке из множества К соответствует одна и только одна точка из множества М. Задача сводится к тому, чтобы найти это единственно возможное соответствие между элементами множеств М и К, т. е. к нахождению трех сплошных линий, соединяющих соответствующие точки множеств.

Принцип решения задачи прост. Если какая-то точка оказывается соединенной с двумя точками другого множества штриховыми линиями, то с его третьей точкой ее необходимо соединить сплошной линией. Поэтому граф на рисунке 2 дополняется сплошными линиями, соединяющими точки Б и р, Р и бр (рис. 3).

 

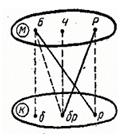
Рис.3

 

Далее остается соединить сплошной линией точку Ч и точку б, так как точка Ч соединена с точкой бр штриховой линией, а точка р уже "занята" (рис. 4).

 

 

Рис. 4

 

Таким образом, на графе этого рисунка автоматически прочитываем ответ: Белокуров — рыжий, Чернов — белокурый, Рыжов – брюнет.

В следующей задаче применение графов помогает обнаружить наличие двух решений.

Задача 3. Маша, Лида, Женя и Катя умеют играть на разных инструментах (виолончели, рояле, гитаре и скрипке), но каждая только на одном. Они же владеют разными иностранными языками (английским, французским, немецким и испанским), но каждая только одним. Известно, что:

1. девушка, которая играет на гитаре, говорит по-испански;

2. Лида не играет ни на скрипке, ни на виолончели и не знает английского языка;

3. Маша не играет ни на скрипке, ни на виолончели и не знает английского языка;

4. девушка, которая говорит по-немецки, не играет на виолончели;

5. Женя знает французский язык, но не играет на скрипке.

Кто на каком инструменте играет и какой иностранный язык знает?

Решение. Условию задачи соответствует граф, изображенный на рисунке

 

 

 

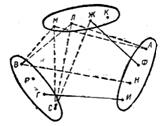
Рис. 5

 

Проведем последовательно следующие сплошные отрезки: КС, ВЖ, ВФ, АК (рис.6).

 

Рис. 6

 

Тем самым образуются два "сплошных" треугольника ЖВФ и КСА. Проводим еще сплошной отрезок РН. Теперь убеждаемся, что условия задачи не обеспечивают однозначности выбора третьей точки для каждой из пар РН и ГИ. Возможны следующие варианты "сплошных" треугольников: МГИ и ЛРН или ЛГИ и МРН. Таким образом, задача имеет два решения.